Paprastosios ir sudėtines palūkanos

Visikreditai.lt 2025 23 rugsėjo

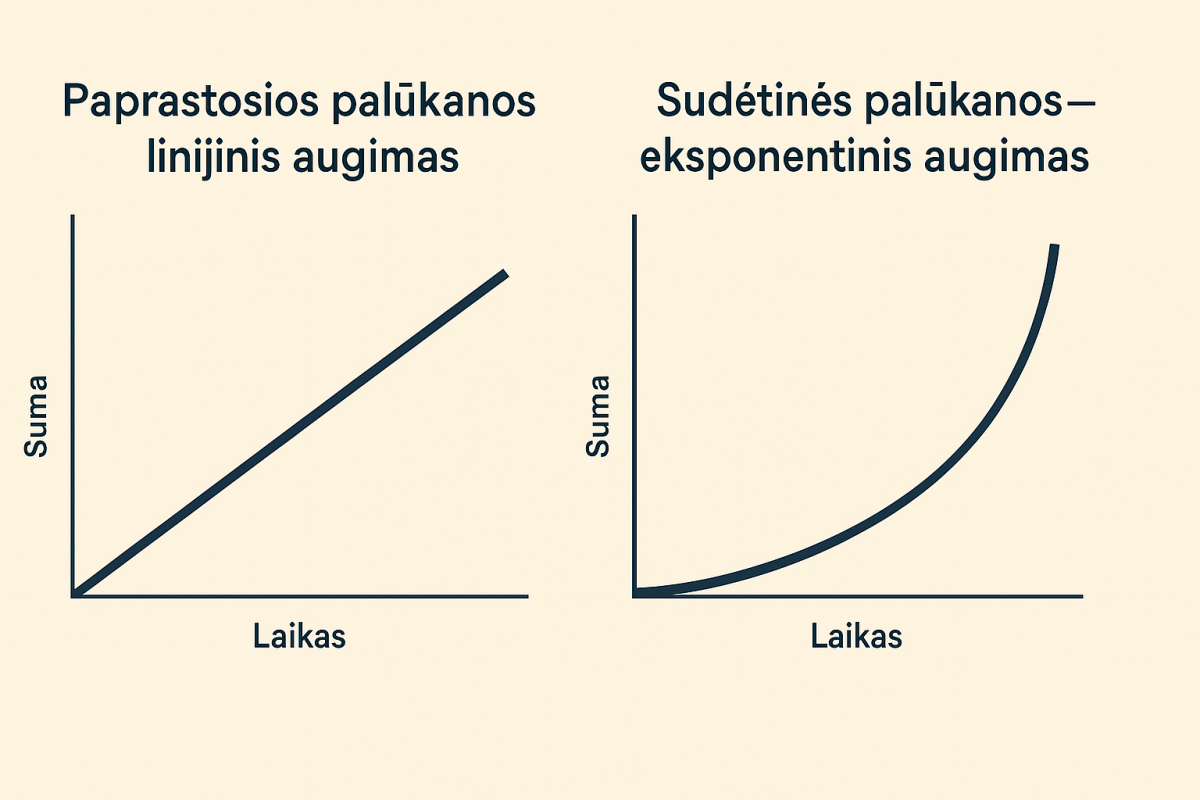
Palūkanos – tai kaina už pinigų naudojimą. Nuo to, kaip jas skaičiuojame, priklauso investicijų augimas, paskolų kaina ir projektų vertinimas. Čia aptarsime dvi bazines schemas – paprastąsias ir sudėtines palūkanas – bei parodysime, kada ir kodėl jos duoda skirtingus rezultatus.

Paprastosios palūkanos

Paprastosios palūkanos – tai palūkanos, skaičiuojamos tik nuo pradinio kapitalo. Jos nekaupia „palūkanų nuo palūkanų“, todėl augimas laikui bėgant yra linijinis. Dažniau taikoma trumpalaikėse paskolose ar ten, kur sutartis aiškiai numato tokias palūkanas.

Paprastųjų palūkanų formulė

Naudojami dydžiai:
P – pradinis kapitalas; r – metinė palūkanų norma (pvz., 5 % = 0,05); t – laikas metais; FV – būsimoji vertė; PV – dabartinė vertė.

Būsimoji vertė (kai skaičiuojame į priekį):
FV = P * (1 + r * t)

Dabartinė vertė (kai diskontuojame iš ateities į šiandieną):
PV = FV / (1 + r * t)

Paprastųjų palūkanų skaičiavimas

Suderinkite vienetus: r – metinė, t – metais.
Įstatykite reikšmes į formulę.
Apskaičiuokite ir, jei reikia, suapvalinkite.

Pavyzdys (būsimoji vertė):
P = 1 000; r = 0,05; t = 3 → FV = 1 000 * (1 + 0,05 * 3) = 1 150,00.

Pavyzdys (dabartinė vertė):
FV = 10 000 po 5 metų; r = 0,06 → PV = 10 000 / (1 + 0,06 * 5) = 7 692,31.

Sudėtinės palūkanos

Sudėtinės palūkanos yra kapitalizuojamos: uždirbtos palūkanos pridedamos prie kapitalo, o kitais laikotarpiais palūkanos skaičiuojamos nuo didesnės sumos. Augimas eksponentinis („palūkanos nuo palūkanų“). Taikoma kai kuriuose indėliuose, investicijose.

Sudėtinių palūkanų formulė

Naudojami dar du dydžiai: m – kapitalizacijos dažnis per metus (pvz., 12 – mėnesinė), EAR/APY – efektyvioji metinė norma.

Diskretinis kaupimas m kartų per metus:
FV = P * (1 + r/m)^(m * t)
PV = FV / (1 + r/m)^(m * t)

Efektyvioji metinė norma (kai nominali r kapitalizuojama m kartų):
EAR = (1 + r/m)^m – 1

Nuolatinis kaupimas:
FV = P * exp(r * t)
PV = FV * exp(-r * t)

Pastaba: „r“ paprastai yra nominali metinė norma. Palyginimui tarp pasiūlymų naudokite EAR/APY.

Sudėtinių palūkanų skaičiavimas

Nustatykite P, r, t ir kapitalizacijos dažnį m (jei nenurodytas – dažniausiai m = 1).
Jei reikia palyginti skirtingus pasiūlymus, pirmiausia perskaičiuokite į EAR.
Apskaičiuokite FV arba PV pagal atitinkamą formulę.

Pavyzdys (tas pats kaip paprastosioms, palyginimui):
P = 1 000; r = 0,05; t = 3.

Metinė kapitalizacija (m = 1): FV = 1 000 * (1 + 0,05)^(3) = 1 157,63.
Mėnesinė kapitalizacija (m = 12): FV = 1 000 * (1 + 0,05/12)^(36) ≈ 1 161,47.

Pavyzdys (diskontavimas su sudėtinėmis):
FV = 10 000 po 5 metų; r = 0,06; m = 1 → PV = 10 000 / (1 + 0,06)^(5) ≈ 7 472,58.

Paprastųjų ir sudėtinių palūkanų palyginimas

Augimo pobūdis: paprastosios – linijinis; sudėtinės – eksponentinis.
Kapitalizacija: paprastųjų nėra; sudėtinių – „palūkanos nuo palūkanų“.
Rezultatas: esant tam pačiam P, r ir t, sudėtinės duoda didesnę FV (ir mažesnę PV diskontuojant).
Kapitalizacijos dažnis: kuo didesnis m, tuo didesnė FV ir efektyvioji metinė norma EAR. Pvz., jei r = 0,10 ir m = 4, tuomet EAR = (1 + 0,10/4)^4 – 1 ≈ 0,1038129 (≈ 10,381 %); kai kapitalizacija nuolatinė, EAR → exp(0,10) – 1 ≈ 10,517 %.
Dvigubėjimo laikas (sudėtinėms): t ≈ ln(2) / ln(1 + r). Apytikslė „72 taisyklė“: t ≈ 72 / (% norma). Pvz., r = 5 % → apie 14,4 metų (tiksliai ≈ 14,21).
Praktinės klaidos: (1) maišoma nominali ir efektyvioji norma; (2) nesuderinti vienetai (metinė r prieš mėnesinius srautus); (3) lyginami pasiūlymai pagal nominalias normas vietoje EAR; (4) ignoruojami mokesčiai ir infliacija (realios grąžos skaičiavimas: 1 + r_reali = (1 + r_nominali) / (1 + infliacija)).

Ką svarbiausia žinoti?

Paprastosios palūkanos – tai linijinis augimas, kai būsimoji vertė skaičiuojama formule FV = P * (1 + r * t); ši schema dažniausiai tinka trumpam laikotarpiui arba kai taip aiškiai numatyta sutartyje.

Sudėtinės palūkanos reiškia palūkanas nuo palūkanų ir eksponentinį augimą: dažniausiai naudojama formulė FV = P * (1 + r/m)^(m * t) arba, esant nuolatinei kapitalizacijai, FV = P * exp(r * t).

Lyginant skirtingus pasiūlymus, pirmiausia verta konvertuoti nominalią normą į efektyviąją metinę normą pagal EAR = (1 + r/m)^m – 1, nes būtent ji leidžia objektyviai palyginti skirtingus kapitalizacijos dažnius. Diskontuojant ateities sumas, sudėtinės palūkanos duoda mažesnę dabartinę vertę nei paprastosios, ypač kai kapitalizacija dažna. Visada suderinkite vienetus (metinė r su t metais; jei srautai mėnesiniai, naudokite m = 12), o vertindami realią grąžą po infliacijos taikykite santykį 1 + r_real = (1 + r_nom) / (1 + infliacija).